Advertisements
Advertisements
प्रश्न
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
विकल्प
1 : 5
1 : 5
1 : 6
3 : 5
उत्तर
Given: (1) AD is the Median of ΔABC
(2) P is a point on AC such that ar (ΔADP) : ar (ΔABD) = `2/3`
To find: ar (ΔPDC) : ar (ΔABC)
We know that” the medians of the triangle divides the triangle in two two triangles of equal area.”
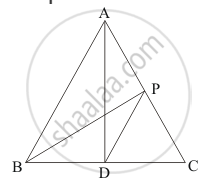
Since AD is the median of ΔABC,
ar (ΔABD) = ar (ΔADC) ……(1)
Also it is given that
ar (ΔADP) : ar (ΔABD) = `2/3` ……(2)
Now,
ar (ΔADC) = ar (ΔADP) + ar (ΔPDC)
ar(ΔADB) = `2/3` ar (ΔADB) + ar (ΔPDC )(from 1 and 2)
ar (ΔPDC ) = `1/3` ar (ΔADB) ..............(3)
ar (ΔABC) = 2ar (ΔADB) ...................(4)
Therefore,
`(ar(ΔPDC))/(ar(ΔABC))= (1/3 ar(ΔADB))/(2ar(ΔADB)`
`(ar(ΔPDC))/(ar(ΔABC))=1/6`
APPEARS IN
संबंधित प्रश्न
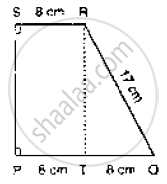
Compute the area of trapezium PQRS is Fig. below.
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
Find the area of a rectangle whose length = 3.6 m breadth = 90 cm
The side of a square field is 16 m. What will be increase in its area, if each of its sides is doubled?
Is the area of your belt the same as the area of the postcard? Why or why not?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 50 boxes. There are 48 fruits in one box.
Tick the one question which matches with the given problem.
Explain why (a) and (c) are not good choices.a) How much will the shopkeeper pay in all? b) How many fruits are there in all? ✓ c) How many more boxes will he need?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 204 eggs. He puts them in egg trays. Each tray has 12 eggs.
a) How many more eggs will he need? b) How many fresh eggs does he sell? c) How many egg trays does he need?
Find the area of the following figure by counting squares:

