Advertisements
Advertisements
प्रश्न
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
उत्तर
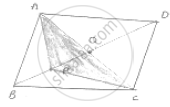
Given that ABCD is a parallelogram
To prove: (1) ar (ΔADO) = ar (ΔCDO)
(2) ar ( ΔABP) = ar (ΔCBP)
Then area (ΔADO) = area (ΔCDO)
Then; area (ΔBAO) area (ΔBCO) ......(1)
In a ΔPAC, Since PO is a median
Then, area (ΔPAO) = area (ΔPCO) ......(2)
⇒ Area (ΔABP) = Area of ΔCBP
APPEARS IN
संबंधित प्रश्न
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
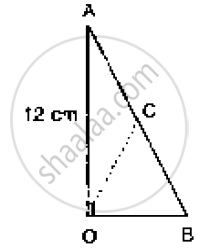
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
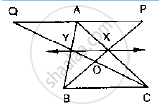
In the below fig. X and Y are the mid-points of AC and AB respectively, QP || BC and
CYQ and BXP are straight lines. Prove that ar (Δ ABP) = ar (ΔACQ).
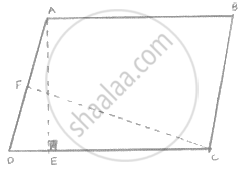
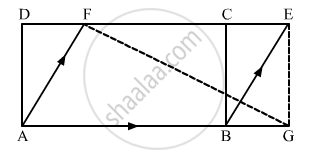
In the given figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

In the given figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ΔEFG.
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
A floor is 40 m long and 15 m broad. It is covered with tiles, each measuring 60 cm by 50 cm. Find the number of tiles required to cover the floor.
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- The cost of one book is Rs 47. Sonu buys 23 books.
a) How much money does she have? b) How much money does she pay for the books? c) What is the cost of 47 books?
