Advertisements
Advertisements
प्रश्न
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
उत्तर
Given: Area (ABC) = 12 cm2, D is midpoint of BC and AP is parallel to ED. We need to find area of the triangle EPC.
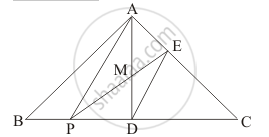
Since, AP||ED, and we know that the area of triangles between the same parallel and on the same base are equal. So,
Area (APE) = Area (APD)
⇒ Area (APM) + Area (AME) = Area (APM) + Area (PMD)
⇒ Area (AME) = Area (PMD) …… (1)
Since, median divide triangles into two equal parts. So,
Area (ADC) = `1/2` Area (ABC) = `12/2` = 6 cm2
⇒ Area (ADC) = Area (MDCE) + Area (AME)
⇒Area (ADC) = Area (MDCE) + Area (PMD) (from equation (1))
⇒ Area (ADC) = Area (PEC)
Therefore,
Area (PEC) = 6 cm2.
APPEARS IN
संबंधित प्रश्न
In fig below, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8
cm and CF = 10 cm, find AD.
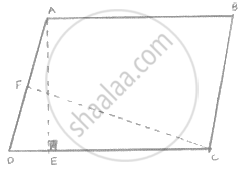
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
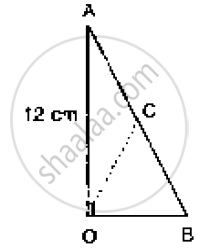
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
D is the mid-point of side BC of ΔABC and E is the mid-point of BD. if O is the mid-point
of AE, prove that ar (ΔBOE) = `1/8` ar (Δ ABC).
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
Find the area of a rectangle whose length and breadth are 25 m and 16 cm.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is increased by 4 m?
How will you decide? Discuss.
