Advertisements
Advertisements
प्रश्न
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
उत्तर
Given: Area (ABC) = 12 cm2, D is midpoint of BC and AP is parallel to ED. We need to find area of the triangle EPC.
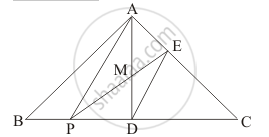
Since, AP||ED, and we know that the area of triangles between the same parallel and on the same base are equal. So,
Area (APE) = Area (APD)
⇒ Area (APM) + Area (AME) = Area (APM) + Area (PMD)
⇒ Area (AME) = Area (PMD) …… (1)
Since, median divide triangles into two equal parts. So,
Area (ADC) = `1/2` Area (ABC) = `12/2` = 6 cm2
⇒ Area (ADC) = Area (MDCE) + Area (AME)
⇒Area (ADC) = Area (MDCE) + Area (PMD) (from equation (1))
⇒ Area (ADC) = Area (PEC)
Therefore,
Area (PEC) = 6 cm2.
APPEARS IN
संबंधित प्रश्न
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
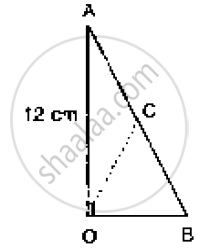
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
Two parallelograms are on the same base and between the same parallels. The ratio of their areas is
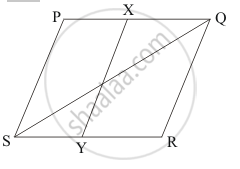
In the given figure, PQRS is a parallelogram. If X and Y are mid-points of PQ and SRrespectively and diagonal Q is joined. The ratio ar (||gm XQRY) : ar (ΔQSR) =
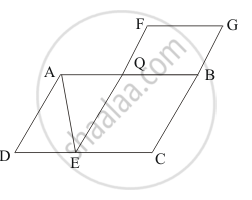
In the given figure, ABCD and FECG are parallelograms equal in area. If ar (ΔAQE) = 12 cm2, then ar (||gm FGBQ) =
The sides of a rectangular park are in the ratio 4 : 3. If its area is 1728 m2, find
(i) its perimeter
(ii) cost of fencing it at the rate of ₹40 per meter.
Is the area of the blue shape more than the area of the yellow shape? Why?

The amount of region enclosed by a plane closed figure is called its ______.
Whose footprint is larger - yours or your friend’s?
Is the area of both your footprints the same?
