Advertisements
Advertisements
Question
P is any point on base BC of ΔABC and D is the mid-point of BC. DE is drawn parallel toPA to meet AC at E. If ar (ΔABC) = 12 cm2, then find area of ΔEPC.
Solution
Given: Area (ABC) = 12 cm2, D is midpoint of BC and AP is parallel to ED. We need to find area of the triangle EPC.
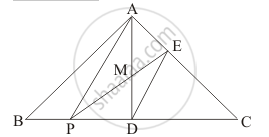
Since, AP||ED, and we know that the area of triangles between the same parallel and on the same base are equal. So,
Area (APE) = Area (APD)
⇒ Area (APM) + Area (AME) = Area (APM) + Area (PMD)
⇒ Area (AME) = Area (PMD) …… (1)
Since, median divide triangles into two equal parts. So,
Area (ADC) = `1/2` Area (ABC) = `12/2` = 6 cm2
⇒ Area (ADC) = Area (MDCE) + Area (AME)
⇒Area (ADC) = Area (MDCE) + Area (PMD) (from equation (1))
⇒ Area (ADC) = Area (PEC)
Therefore,
Area (PEC) = 6 cm2.
APPEARS IN
RELATED QUESTIONS
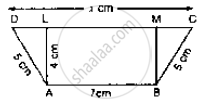
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that:
ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar (ΔBPC)
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
In below fig., PSDA is a parallelogram in which PQ = QR = RS and AP || BQ || CR. Prove
that ar (Δ PQE) = ar (ΔCFD).
A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
Find the area of a square, whose side is: 4.5 cm.
Look at a 10 rupee note. Is its area more than hundred square cm?
Altogether how many squares can be arranged on it?
Measure the length of the floor of your classroom in meters. Also, measure the width.
- So how many children can sit in one square meter?
Find the area of the following figure by counting squares:

