Question

ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ: QP = 3.1. If ar (ΔPBQ) = 10cm², find the area of parallelogram ABCD.

Answer 1

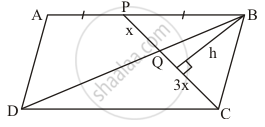
Proof:

Let, CQ = 3x & PQ = x

ar (ΔPBQ) = 10cm²         ...(1)

We know that, Area of Δ = ½ × Base × Height

ar (∆PBQ) = ½ × PQ × BQ

10 = ½ × x × h

[Let BQ = h ]

10 × 2 = xh

xh = 20                 ...(2)

ar (∆BQC) = ½ × QC × BQ

ar (∆BQC) = ½ × 3(x × h)

ar (∆BQC) = ½ × 3 × 20

[From eq 2]

ar (∆BQC) = 3 × 10

ar (∆BQC) = 30 cm²         ...(3) 

Now,

ar (∆PCB) = ar (∆PBQ) + ar (∆BQC)

ar (∆PCB) = 10 + 30

[From eq 1 & 3]

ar (∆PCB) = 40 cm²

½ × PB × BC = 40 cm²

PB × BC = (40 × 2) cm²

PB × BC = 80 cm²        ...(4)

Now, area of parallelogram = Base × Height

ar (|| gm ABCD) = AB × BC

ar (|| gm ABCD) = 2 PB × BC

[AB = 2 BP , P is the mid point of AB]

Area (ABCD) = 2 × 80

[From eq 4]

ar (ABCD) = 160 cm² 

Hence, the area of parallelogram ABCD is 160 cm².