Advertisements
Advertisements
प्रश्न
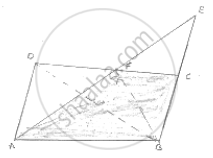
ABCD is a parallelogram in which BC is produced to E such that CE = BC. AE intersects
CD at F.
(i) Prove that ar (ΔADF) = ar (ΔECF)
(ii) If the area of ΔDFB = 3 cm2, find the area of ||gm ABCD.
Advertisements
उत्तर
In triangles and , ADF ECF we have
∠ADF = ∠ECF [Alternative interior angles, Since || AD BE]
AD = EC [ Since AD = BC = CE ]
And ∠DFA = ∠CFA [vertically opposite angles]
So, by AAS congruence criterion, we have
ΔADF ≅ ECF
⇒ area (ΔADF) = area (ΔECF) and DF = CF.
Now, DF = CF
⇒ BF is a madian in ΔBCD
⇒ area (ΔBCD) =2ar (ΔBDF)
⇒ area (ΔBCD) = 2× 3 cm2 =6cm2
Hence, ar (||gm ABCD) = 2ar (ΔBCD) 2 × 6cm2
=12cm2
APPEARS IN
संबंधित प्रश्न
ABCD is a parallelogram whose diagonals AC and BD intersect at O. A line through O
intersects AB at P and DC at Q. Prove that ar (Δ POA) = ar (Δ QOC).
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
ABCD is a parallelogram. P is any point on CD. If ar (ΔDPA) = 15 cm2 and ar (ΔAPC) = 20 cm2, then ar (ΔAPB) =
ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
ABCD is a trapezium with parallel sides AB =a and DC = b. If E and F are mid-points of non-parallel sides AD and BC respectively, then the ratio of areas of quadrilaterals ABFEand EFCD is
The length and breadth of a rectangular piece of land are in the ratio 5 : 3. If the total cost of fencing it at the rate of ₹24 per meter is ₹9600, find its :
(i) length and breadth
(ii) area
(iii) cost of levelling at the rate of ₹60 per m2.
Find the area of a rectangle whose length = 24 cm breadth =180 mm
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri, and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.
- Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
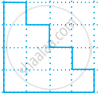
Find the area of the following figure by counting squares:
Find the area of the following figure by counting squares:
