Advertisements
Advertisements
प्रश्न
Who had the bigger piece? How much bigger?
उत्तर
So, the area of piece B is bigger than the area of piece A.
The difference in the area of piece A and piece B
= 33 - 30
= 3 square cm
So, piece B is 3 square cm bigger than piece A.
APPEARS IN
संबंधित प्रश्न
In Q. No 1, if AD = 6 cm, CF = 10 cm, and AE = 8cm, find AB.
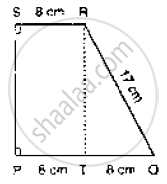
Compute the area of trapezium PQRS is Fig. below.
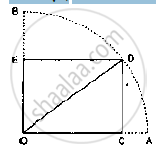
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
In the below Fig, ABC and ABD are two triangles on the base AB. If line segment CD is
bisected by AB at O, show that ar (Δ ABC) = ar (Δ ABD)

If P is any point in the interior of a parallelogram ABCD, then prove that area of the
triangle APB is less than half the area of parallelogram.
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove
that: (1) ar (ΔADO) = ar (ΔCDO) (2) ar (ΔABP) = ar (ΔCBP)
In the given figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

A triangle and a parallelogram are on the same base and between the same parallels. The ratio of the areas of triangle and parallelogram is
Let ABC be a triangle of area 24 sq. units and PQR be the triangle formed by the mid-points of the sides of Δ ABC. Then the area of ΔPQR is
In the given figure, ABCD is a parallelogram. If AB = 12 cm, AE = 7.5 cm, CF = 15 cm, then AD =

ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
The perimeter of a triangle ABC is 37 cm and the ratio between the lengths of its altitudes be 6: 5: 4. Find the lengths of its sides.
Let the sides be x cm, y cm, and (37 - x - y) cm. Also, let the lengths of altitudes be 6a cm, 5a cm, and 4a cm.
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
Find the area of a rectangle whose length = 3.6 m breadth = 90 cm
Find the area of a square, whose side is: 4.5 cm.
Find the area of a square, whose side is: 4.1 cm.
The side of a square field is 16 m. What will be increase in its area, if each of its sides is doubled?
By counting squares, estimate the area of the figure.

The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| 13 cm | ? | 54 cm | ? |
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| ? | 15 cm | 60 cm | ? |
Altogether how many squares can be arranged on it?
So the area of piece A = ________ square cm
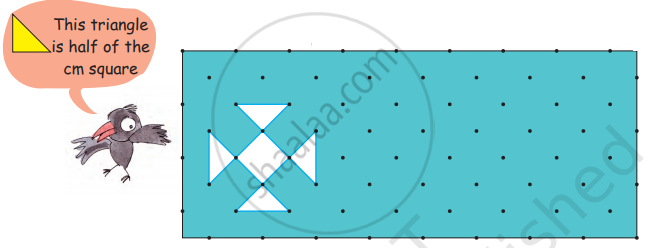
How many tiles like the triangle given here will fit in the white design?
Area of design = ________ square cm
Measure the length of the floor of your classroom in meters. Also, measure the width.
- What is the area of the floor of your classroom in square metres?
Nasreena is a farmer who wants to divide her land equally among her three children — Chumki, Jhumri, and Imran. She wants to divide the land so that each piece of land has one tree. Her land looks like this.
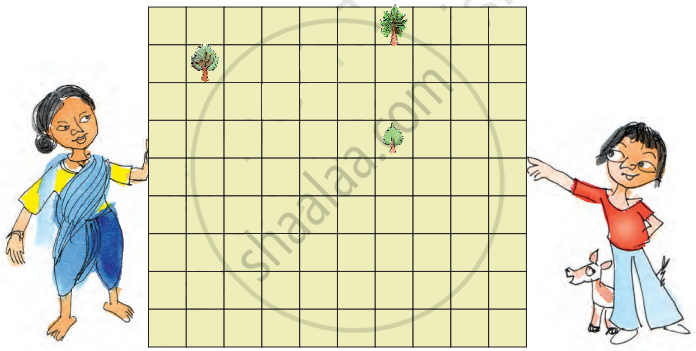
- Can you divide the land equally? Show how you will divide it. Remember each person has to get a tree. Colour each person’s piece of land differently.
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- The cost of one book is Rs 47. Sonu buys 23 books.
a) How much money does she have? b) How much money does she pay for the books? c) What is the cost of 47 books?
An engineer who plans to build a compound wall on all sides of a house must find the area of the compound.
Find the area of the following figure by counting squares:

