Advertisements
Advertisements
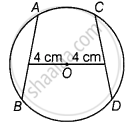
Question
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Options
True
False
Solution
This statement is True.
Explanation:
Because, the chords equidistant from the centre of circle are equal in length.
APPEARS IN
RELATED QUESTIONS
If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
true or false
If a circle is divided into three equal arcs each is a major arc.
Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
Angle formed in minor segment of a circle is
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
Two equal circles of radius r intersect such that each passes through the centre of the other. The length of the common chord of the circle is
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is
Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
