Advertisements
Advertisements
Question
Find the length of a chord which is at a distance of 5 cm from the centre of a circle ofradius 10 cm.
Solution
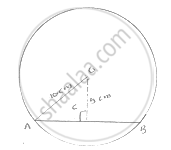
Given that
Distance (OC)=5cm
Radius of circle (OA)10cm
In OCA by Pythagoras theorem
`AC^2+OC^2=OA^2`
`⇒AC^2+5^2=10^2`
`⇒AC=sqrt75=8.66cm`
WRK, the perpendicular from center to chord bisects the chord
`∴AC=BC=8.66cm`
Then chord AB=8.66+8.66
= 17.32 cm
APPEARS IN
RELATED QUESTIONS
If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
true or false
A circle has only finite number of equal chords.
An equilateral triangle of side 9cm is inscribed in a circle. Find the radius of the circle.
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its center. If the distance between AB and CD is 6 cm. Find the radius of the circle.
In a circle of radius 17 cm, two parallel chords are drawn on opposite side of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is
Two chords AB and CD of a circle are each at distances 4 cm from the centre. Then AB = CD.
Two chords AB and AC of a circle with centre O are on the opposite sides of OA. Then ∠OAB = ∠OAC .
Two congruent circles with centres O and O′ intersect at two points A and B. Then ∠AOB = ∠AO′B.
If two equal chords of a circle intersect, prove that the parts of one chord are separately equal to the parts of the other chord.
AB and AC are two chords of a circle of radius r such that AB = 2AC. If p and q are the distances of AB and AC from the centre, prove that 4q2 = p2 + 3r2.
