Advertisements
Advertisements
Question
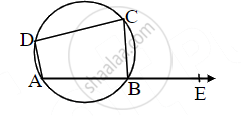
In the figure, ▢ABCD is a cyclic quadrilateral. If m(arc ABC) = 230°, then find ∠ABC, ∠CDA, ∠CBE.
Solution
m(arc ABC) = 230° .....(i) [Given]
∴ m(arc ADC) + m(arc ABC) = 360° .......[Degree measure of a circle is 360°]
∴ m(arc ADC) = 360° – m(arc ABC)
∴ m(arc ADC) = 360° – 230° .......[From (i)]
∴ m(arc ADC) = 130°
∠ABC = `1/2` m (arc ADC) ......[Inscribed angle theorem]
= `1/2 xx 130^circ`
= 65°
Now, ∠CDA = `1/2` m (arc ABC) ......[Inscribed angle theorem]
∴ ∠CDA = `1/2 xx 230^circ`
∴ ∠CDA = 115° ......(ii)
∠CBE = ∠CDA ......(iiii) [The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle]
∴ ∠CBE = 115° .....[From (ii) and (iii)]
∴ ∠ABC = 65°, ∠CDA = 115°, ∠CBE = 115°.
RELATED QUESTIONS
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, find ∠BCD. Further, if AB = BC, find ∠ECD.
ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD = ∠CBD.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are equal.
In the given figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.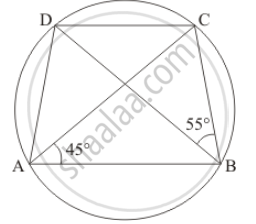
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that EB = EC.
In the given figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.

PQRS is a cyclic quadrilateral such that PR is a diameter of the circle. If ∠QPR = 67° and ∠SPR = 72°, then ∠QRS =
Find all the angles of the given cyclic quadrilateral ABCD in the figure.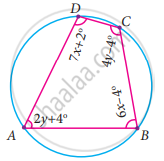
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140º, then ∠BAC is equal to ______.
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If a pair of opposite sides of a cyclic quadrilateral are equal, prove that its diagonals are also equal.
The three angles of a quadrilateral are 100°, 60°, 70°. Find the fourth angle.
