Advertisements
Advertisements
Question
Two circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see the given figure). Prove that ∠ACP = ∠QCD.

Solution
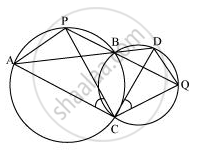
Join chords AP and DQ.
For chord AP,
∠PBA = ∠ACP (Angles in the same segment) ... (1)
For chord DQ,
∠DBQ = ∠QCD (Angles in the same segment) ... (2)
ABD and PBQ are line segments intersecting at B.
∴ ∠PBA = ∠DBQ (Vertically opposite angles) ... (3)
From equations (1), (2), and (3), we obtain
∠ACP = ∠QCD
APPEARS IN
RELATED QUESTIONS
Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.
Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
Prove that the circle drawn with any side of a rhombus as diameter passes through the point of intersection of its diagonals.
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.
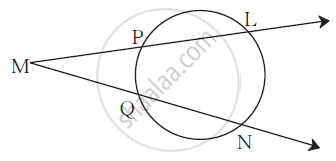
In the figure m(arc LN) = 110°,
m(arc PQ) = 50° then complete the following activity to find ∠LMN.
∠ LMN = `1/2` [m(arc LN) - _______]
∴ ∠ LMN = `1/2` [_________ - 50°]
∴ ∠ LMN = `1/2` × _________
∴ ∠ LMN = __________
Prove that the circles described on the four sides of a rhombus as diameters, pass through the point of intersection of its diagonals.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
ABCD is a cyclic quadrilateral such that ∠ADB = 30° and ∠DCA = 80°, then ∠DAB =
ABCD is a cyclic quadrilateral such that ∠A = 90°, ∠B = 70°, ∠C = 95° and ∠D = 105°.
If bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
