Advertisements
Advertisements
प्रश्न
In ΔPQR, ∠P = 30°, ∠Q = 60°, ∠R = 90° and PQ = 12 cm, then find PR and QR.
उत्तर
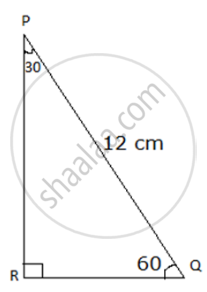
From figure using the definition of sin
sin∠P = `"RQ"/"PQ"`
∴ sin30° = `"RQ"/12`
∴ `1/2 = "RQ"/12`
∴ RQ = 12/2 = 6 cm
∴ QR = 6 cm
sin∠Q = `"PR"/"PQ"`
∴ sin 60° = `"PR"/12`
∴ `sqrt(3)/2 = "PR"/12`
∴ PR = `(12sqrt(3))/2`
∴ PR = `6sqrt3` cm
Therefore PR = `6sqrt3` cm and QR = 6 cm
APPEARS IN
संबंधित प्रश्न
If \[\cot\theta = \frac{40}{9}\], find the values of cosecθ and sinθ.
Prove that:
Prove that:
Prove that: `1/"sec θ − tan θ" = "sec θ + tan θ"`
Prove that:
Choose the correct alternative answer for the following question.
sin \[\theta\] cosec \[\theta\]= ?
Choose the correct alternative answer for the following question.
cosec 45° =?
Choose the correct alternative answer for the following question.
1 + tan2 \[\theta\] = ?
Choose the correct alternative answer for the following question.
Prove the following.
(secθ + tanθ) (1 – sinθ) = cosθ
Prove the following.
cot2θ – tan2θ = cosec2θ – sec2θ
Prove the following.
Prove the following:
sec6x – tan6x = 1 + 3sec2x × tan2x
Prove the following.
\[\frac{\tan\theta}{\sec\theta + 1} = \frac{\sec\theta - 1}{\tan\theta}\]
Choose the correct alternative:
sinθ × cosecθ =?
ΔAMT∼ΔAHE, construct Δ AMT such that MA = 6.3 cm, ∠MAT=120°, AT = 4.9 cm and `"MA"/"HA"=7/5`, then construct ΔAHE.
