Advertisements
Advertisements
Question
In ΔPQR, ∠P = 30°, ∠Q = 60°, ∠R = 90° and PQ = 12 cm, then find PR and QR.
Solution
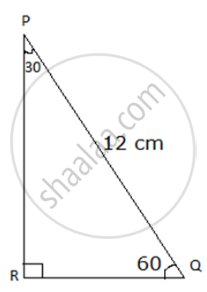
From figure using the definition of sin
sin∠P = `"RQ"/"PQ"`
∴ sin30° = `"RQ"/12`
∴ `1/2 = "RQ"/12`
∴ RQ = 12/2 = 6 cm
∴ QR = 6 cm
sin∠Q = `"PR"/"PQ"`
∴ sin 60° = `"PR"/12`
∴ `sqrt(3)/2 = "PR"/12`
∴ PR = `(12sqrt(3))/2`
∴ PR = `6sqrt3` cm
Therefore PR = `6sqrt3` cm and QR = 6 cm
APPEARS IN
RELATED QUESTIONS
If \[\tan \theta = \frac{3}{4}\], find the values of secθ and cosθ
If \[\cot\theta = \frac{40}{9}\], find the values of cosecθ and sinθ.
Prove that:
cos2θ (1 + tan2θ)
Prove that:
Prove that:
(secθ - cosθ)(cotθ + tanθ) = tanθ.secθ.
Prove that:
Choose the correct alternative answer for the following question.
sin \[\theta\] cosec \[\theta\]= ?
Choose the correct alternative answer for the following question.
1 + tan2 \[\theta\] = ?
Prove the following.
secθ (1 – sinθ) (secθ + tanθ) = 1
Prove the following.
(secθ + tanθ) (1 – sinθ) = cosθ
Prove the following.
sec2θ + cosec2θ = sec2θ × cosec2θ
Prove the following.
cot2θ – tan2θ = cosec2θ – sec2θ
Prove the following.
If sinθ = `8/17`, where θ is an acute angle, find the value of cos θ by using identities.
Show that:
`sqrt((1-cos"A")/(1+cos"A"))=cos"ecA - cotA"`
Prove that: (sec θ – cos θ) (cot θ + tan θ) = tan θ.sec θ
Proof: L.H.S. = (sec θ – cos θ) (cot θ + tan θ)
= `(1/square - cos θ) (square/square + square/square)` ......`[∵ sec θ = 1/square, cot θ = square/square and tan θ = square/square]`
= `((1 - square)/square) ((square + square)/(square square))`
= `square/square xx 1/(square square)` ......`[(∵ square + square = 1),(∴ square = 1 - square)]`
= `square/(square square)`
= tan θ.sec θ
= R.H.S.
∴ L.H.S. = R.H.S.
∴ (sec θ – cos θ) (cot θ + tan θ) = tan θ.sec θ
