Advertisements
Advertisements
प्रश्न
ΔAMT∼ΔAHE, construct Δ AMT such that MA = 6.3 cm, ∠MAT=120°, AT = 4.9 cm and `"MA"/"HA"=7/5`, then construct ΔAHE.
उत्तर
Δ AMT and Δ AHE are give
⇒ `("MA")/("HA")= ("AT")/("AE") =("TM")/("EH")=7/5`
⇒ `("MA")/("HA")=7/5 ⇒ 6.3/"HA" =7/5`
⇒ `"HA" =(6.3xx5)/7`
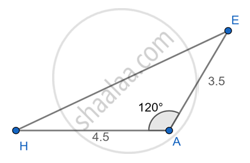
⇒ HA = 4.5cm
Similarly, `"AT"/"AE" =7/5`
⇒ `4.9/"AE" =7/5 ⇒"AE" =(4.9xx5)/7⇒"AE"=3.5`cm
Given triangle Required triangle
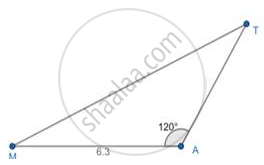
Steps of Constructing the required triangle:
1. Draw a line segment of some length HP and mark an arc of 4.5cm(as calculated above) and name it as A.

2. At vertex A, make an angle of 120°
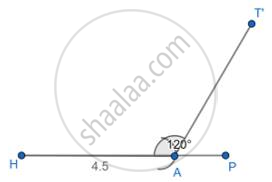
3. Mark an arc of 3.5cm (as calculated above) on AT’ and name it E.
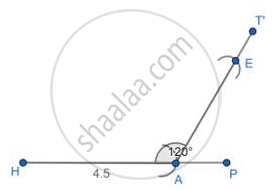
4. Join HE.
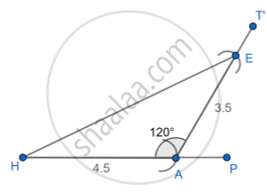
5. Δ AHE is the required triangle.
APPEARS IN
संबंधित प्रश्न
If tanθ = 1 then, find the value of
`(sinθ + cosθ)/(secθ + cosecθ)`
Prove that:
Prove that:
(secθ - cosθ)(cotθ + tanθ) = tanθ.secθ.
Prove that:
Prove that: `1/"sec θ − tan θ" = "sec θ + tan θ"`
Prove that:
Choose the correct alternative answer for the following question.
cosec 45° =?
Choose the correct alternative answer for the following question.
1 + tan2 \[\theta\] = ?
Choose the correct alternative answer for the following question.
Prove the following.
secθ (1 – sinθ) (secθ + tanθ) = 1
Prove the following.
(secθ + tanθ) (1 – sinθ) = cosθ
Prove the following.
cot2θ – tan2θ = cosec2θ – sec2θ
Prove the following.
Prove the following:
sec6x – tan6x = 1 + 3sec2x × tan2x
If sinθ = `8/17`, where θ is an acute angle, find the value of cos θ by using identities.
Show that:
`sqrt((1-cos"A")/(1+cos"A"))=cos"ecA - cotA"`
