NCERT Exemplar solutions for Mathematics [English] Class 9 chapter 5 - Introduction To Euclid's Geometry [Latest edition]

The three steps from solids to points are ______.

The number of dimensions, a solid has ______.

The number of dimensions, a surface has ______.

The number of dimension, a point has ______.

Euclid divided his famous treatise “The Elements” into ______.

The total number of propositions in the Elements are ______.

Boundaries of solids are ______.

Boundaries of surfaces are ______.

In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio ______.

A pyramid is a solid figure, the base of which is ______.

The side faces of a pyramid are ______.

It is known that if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is ______.

In ancient India, the shapes of altars used for household rituals were ______.

The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is ______.

Greek’s emphasised on ______.

In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for ______.

Euclid belongs to the country ______.

Thales belongs to the country ______.

Pythagoras was a student of ______.

Which of the following needs a proof?

Euclid stated that all right angles are equal to each other in the form of ______.

‘Lines are parallel, if they do not intersect’ is stated in the form of ______.

Euclidean geometry is valid only for curved surfaces.

The boundaries of the solids are curves.

The edges of a surface are curves.

The things which are double of the same thing are equal to one another.

If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.

The statements that are proved are called axioms.

“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.

Two distinct intersecting lines cannot be parallel to the same line.

Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.

Solve the following question using appropriate Euclid’s axiom:

Two salesmen make equal sales during the month of August. In September, each salesman doubles his sale of the month of August. Compare their sales in September.

Solve the following question using appropriate Euclid’s axiom:

It is known that x + y = 10 and that x = z. Show that z + y = 10?

Solve the following question using appropriate Euclid’s axiom:

Look at the figure. Show that length AH > sum of lengths of AB + BC + CD.

Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have AB = BC, BX = BY. Show that AX = CY.

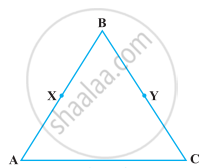
Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.

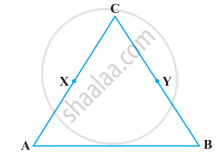
Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.

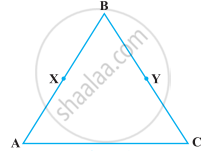
Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have ∠1 = ∠2, ∠2 = ∠3. Show that ∠1 = ∠3.

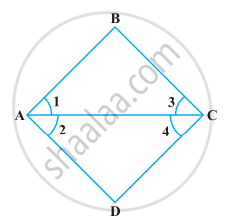
Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.

Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2.

Solve the following question using appropriate Euclid’s axiom:

In the following figure, we have AC = DC, CB = CE. Show that AB = DE.

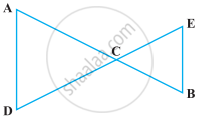
Solve the following question using appropriate Euclid’s axiom:

In the following figure, if OX = `1/2` XY, PX = `1/2` XZ and OX = PX, show that XY = XZ.

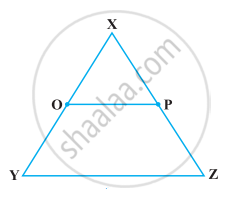
In the following figure AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.

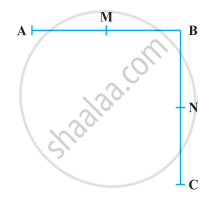
In the following figure BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

Read the following statement :

An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.

Study the following statement:

“Two intersecting lines cannot be perpendicular to the same line”.

Check whether it is an equivalent version to the Euclid’s fifth postulate.

[Hint: Identify the two intersecting lines l and m and the line n in the above statement.]

Read the following statements which are taken as axioms:

1. If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
2. If a transversal intersect two parallel lines, then alternate interior angles are equal. 

Is this system of axioms consistent? Justify your answer.

Read the following two statements which are taken as axioms:

1. If two lines intersect each other, then the vertically opposite angles are not equal.
2. If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.

Is this system of axioms consistent? Justify your answer.

Read the following axioms:

1. Things which are equal to the same thing are equal to one another.
2. If equals are added to equals, the wholes are equal.
3. Things which are double of the same thing are equal to one another.

Check whether the given system of axioms is consistent or inconsistent.