Advertisements
Advertisements
Question
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
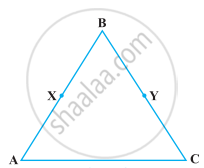
Solution
We have, AB = BC ...(i)
And BX = BY ...(ii)
According to Euclid’s axiom, if equals are subtracted from equals, the remainders are equal.
So, on subtracting equation (ii) from equation (i), we get
AB – BX = BC – BY
⇒ AX = CY ...[From figure]
APPEARS IN
RELATED QUESTIONS
The following statement is true or false? Give reason for your answer.
Only one line can pass through a single point.
How many lines can be drawn through both of the given points?
In how many points a line, not in a plane, can intersect the plane?
How many least number of distinct points determine a unique plane?
How many planes can be made to pass through three distinct points?
The things which are double of the same thing are equal to one another.
If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
The following statement is true or false? Give reason for your answer.
There are an infinite number of lines which pass through two distinct points.
