Advertisements
Advertisements
Question
How many least number of distinct points determine a unique plane?
Solution
If we have two distinct points, then we can draw infinite number of planes passing through those two points. While if we have three distinct non collinear points, only a single unique plane can be drawn passing through those three points.
Therefore, a minimum of three distinct non collinear points are required to get a unique plane.
APPEARS IN
RELATED QUESTIONS
How many planes can be made to pass through three distinct points?
The number of dimensions, a solid has ______.
The number of dimension, a point has ______.
Boundaries of solids are ______.
The side faces of a pyramid are ______.
In ancient India, the shapes of altars used for household rituals were ______.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
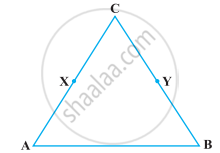
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2.

In the following figure BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

The following statement is true or false? Give reason for your answer.
There are an infinite number of lines which pass through two distinct points.
