Advertisements
Advertisements
Question
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
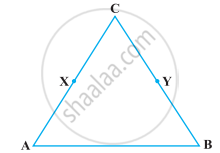
Solution
Given, X is the mid-point of AC
AX = CX = `1/2` AC
⇒ 2AX = 2CX = AC ...(i)
And Y is the mid-point of BC.
BY = CY = `1/2` BC
⇒ 2BY = 2CY = BC ...(ii)
Also, given AX = CY ...(iii)
According to Euclid’s axiom, things which are double of the same things are equal to one another.
From equation (iii), 2AX = 2CY
⇒ AC = BC ...[From equation (i) and (ii)]
APPEARS IN
RELATED QUESTIONS
How many least number of distinct points determine a unique plane?
How many planes can be made to pass through a line and a point not on the line?
It is known that if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is ______.
Euclid belongs to the country ______.
Which of the following needs a proof?
The boundaries of the solids are curves.
The statements that are proved are called axioms.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Solve the following question using appropriate Euclid’s axiom:
It is known that x + y = 10 and that x = z. Show that z + y = 10?
Read the following axioms:
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
