Advertisements
Advertisements
Question
Solve the following question using appropriate Euclid’s axiom:
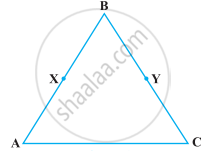
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.
Solution
Given, BX = `1/2` AB
⇒ 2BX = AB ...(i)
BY = `1/2` BC
⇒ 2BY = BC ...(ii)
And AB = BC ...(iii)
On putting the values from equations (i) and (ii) in equation (iii), we get
2BX = 2BY
According to Euclid’s axiom, things which are double of the same things are equal to one another.
BX = BY
APPEARS IN
RELATED QUESTIONS
How many lines can be drawn through a given point.
Given three distinct points in a plane, how many lines can be drawn by joining them?
How many planes can be made to pass through two points?
A pyramid is a solid figure, the base of which is ______.
The side faces of a pyramid are ______.
It is known that if x + y = 10 then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is ______.
The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is ______.
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
Solve the following question using appropriate Euclid’s axiom:
It is known that x + y = 10 and that x = z. Show that z + y = 10?
Solve the following question using appropriate Euclid’s axiom:
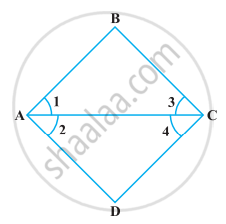
In the following figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.