Advertisements
Advertisements
Question
How many lines can be drawn through a given point.
Solution
Given a single point, then we can draw infinite number of lines through that point.
For example: If we have a point A, then there are infinite numbers of lines passing through it.

Here, lines m, n, o and p all pass through point A.
APPEARS IN
RELATED QUESTIONS
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Given three distinct points in a plane, how many lines can be drawn by joining them?
How many planes can be made to pass through a line and a point not on the line?
Boundaries of solids are ______.
Euclid stated that all right angles are equal to each other in the form of ______.
The boundaries of the solids are curves.
If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Solve the following question using appropriate Euclid’s axiom:
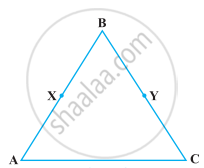
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.