Advertisements
Advertisements
Question
How many lines can be drawn through both of the given points?
Solution
Given two distinct points, only one unique line can be drawn passing through both of them.
For example, if we have two distinct points A and B, only one line is there which passes through both of them.

APPEARS IN
RELATED QUESTIONS
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
The number of dimensions, a surface has ______.
Boundaries of surfaces are ______.
Greek’s emphasised on ______.
Euclid belongs to the country ______.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Solve the following question using appropriate Euclid’s axiom:
Two salesmen make equal sales during the month of August. In September, each salesman doubles his sale of the month of August. Compare their sales in September.
Solve the following question using appropriate Euclid’s axiom:
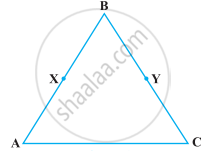
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.
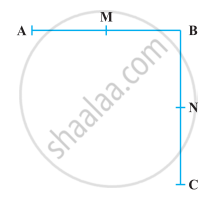
In the following figure AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.
Read the following statement :
An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.
