Advertisements
Advertisements
Question
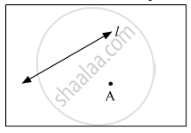
How many planes can be made to pass through a line and a point not on the line?
Solution
Given a line and a distinct point not lying on the line, only a single plane can be drawn through both of them as there can be only plane which can accommodate both the line and the point together.
Let us take a line l and a point A, as we can see there can be only plane which pass through both of them.
APPEARS IN
RELATED QUESTIONS
In how many points a line, not in a plane, can intersect the plane?
In how many lines two distinct planes can intersect?
How many least number of distinct points determine a unique plane?
Euclid stated that all right angles are equal to each other in the form of ______.
The boundaries of the solids are curves.
The edges of a surface are curves.
Solve the following question using appropriate Euclid’s axiom:
It is known that x + y = 10 and that x = z. Show that z + y = 10?
Solve the following question using appropriate Euclid’s axiom:
Look at the figure. Show that length AH > sum of lengths of AB + BC + CD.

Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.
In the following figure BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

