Advertisements
Advertisements
Question
Solve the following question using appropriate Euclid’s axiom:
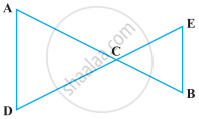
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.
Solution
Given, AC = DC ...(i)
And C6 = CE ...(ii)
According to Euclid’s axiom, if equals are added to equals, then wholes are also equal.
So, on adding equation (i) and (ii), we get
AC + CB = DC + CE
⇒ AB = DE
APPEARS IN
RELATED QUESTIONS
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
If a point C lies between two points A and B such that AC = BC, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
How many lines can be drawn through both of the given points?
In how many lines two distinct planes can intersect?
Thales belongs to the country ______.
Solve the following question using appropriate Euclid’s axiom:
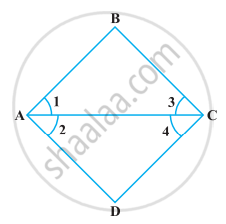
In the following figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.
Read the following axioms:
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
The following statement is true or false? Give reason for your answer.
There are an infinite number of lines which pass through two distinct points.
The following statement is true or false? Give reason for your answer.
A terminated line can be produced indefinitely on both the sides.
