Advertisements
Advertisements
Question
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.
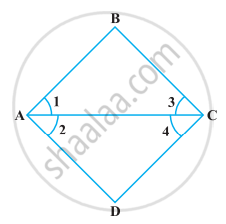
Solution
Given, ∠1 = ∠3 ...(i)
And ∠2 = ∠4 ...(ii)
According to Euclid’s axiom, if equals are added to equals, then wholes are also equal.
On adding equations (i) and (ii), we get
∠1 + ∠2 = ∠3 + ∠4
⇒ ∠A = ∠C
APPEARS IN
RELATED QUESTIONS
The following statement is true or false? Give reason for your answer.
Only one line can pass through a single point.
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
parallel lines
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
line segment
Consider two ‘postulates’ given below:-
- Given any two distinct points A and B, there exists a third point C which is in between A and B.
- There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
In how many lines two distinct planes can intersect?
Given three distinct points in a plane, how many lines can be drawn by joining them?
Euclid divided his famous treatise “The Elements” into ______.
Boundaries of surfaces are ______.
The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is ______.
