Advertisements
Advertisements
Question
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2.

Solution
Given, ∠ABC = ∠ACB ...(i)
And ∠4 = ∠3 ...(ii)
According to Eulid’s axiom, if equals are subtracted from equals, then remainders are also equal.
On subtracting equation (ii) from equation (i), we get
∠ABC – ∠4 = ∠ACB – ∠3
⇒ ∠1 = ∠2
Now, in ABDC, ∠1 = ∠2
⇒ DC = BD ...[Sides opposite to equal angles are equal]
BD = DC.
APPEARS IN
RELATED QUESTIONS
The following statement is true or false? Give reason for your answer.
Only one line can pass through a single point.
The three steps from solids to points are ______.
A pyramid is a solid figure, the base of which is ______.
If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
The statements that are proved are called axioms.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.
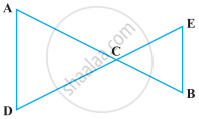
Solve the following question using appropriate Euclid’s axiom:
In the following figure, if OX = `1/2` XY, PX = `1/2` XZ and OX = PX, show that XY = XZ.
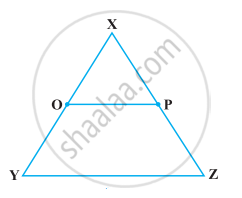
Read the following statements which are taken as axioms:
- If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
- If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
Read the following axioms:
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
The following statement is true or false? Give reason for your answer.
In the following figure, if AB = PQ and PQ = XY, then AB = XY.

