Advertisements
Advertisements
Question
Read the following statements which are taken as axioms:
- If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
- If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
Solution
A system of axiom is called consistent, if there is no statement which can be deduced from these axioms such that it contradicts any axiom. We know that, if a transversal intersects two parallel lines, then each pair of corresponding angles are equal, which is a theorem. So, Statement I is false and not an axiom.
Also, we know that, if a transversal intersects two parallel lines, then each pair of alternate interior angles are equal. It is also a theorem. So, Statement II is true and an axiom.
Thus, in given statements, first is false and second is an axiom.
Hence, given system of axioms is not consistent.
APPEARS IN
RELATED QUESTIONS
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
radius of a circle
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
square
In how many points two distinct lines can intersect?
The total number of propositions in the Elements are ______.
In ancient India, the shapes of altars used for household rituals were ______.
The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is ______.
In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for ______.
The edges of a surface are curves.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
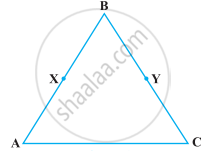
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.