Advertisements
Advertisements
प्रश्न
Read the following statements which are taken as axioms:
- If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
- If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
उत्तर
A system of axiom is called consistent, if there is no statement which can be deduced from these axioms such that it contradicts any axiom. We know that, if a transversal intersects two parallel lines, then each pair of corresponding angles are equal, which is a theorem. So, Statement I is false and not an axiom.
Also, we know that, if a transversal intersects two parallel lines, then each pair of alternate interior angles are equal. It is also a theorem. So, Statement II is true and an axiom.
Thus, in given statements, first is false and second is an axiom.
Hence, given system of axioms is not consistent.
APPEARS IN
संबंधित प्रश्न
How many least number of distinct points determine a unique plane?
How many planes can be made to pass through two points?
The number of dimension, a point has ______.
A pyramid is a solid figure, the base of which is ______.
The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is ______.
Euclid belongs to the country ______.
The edges of a surface are curves.
The statements that are proved are called axioms.
Attempts to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
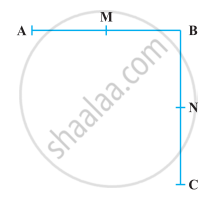
In the following figure AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.