Advertisements
Advertisements
प्रश्न
Solve the following question using appropriate Euclid’s axiom:
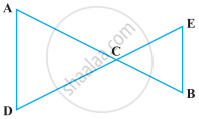
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.
उत्तर
Given, AC = DC ...(i)
And C6 = CE ...(ii)
According to Euclid’s axiom, if equals are added to equals, then wholes are also equal.
So, on adding equation (i) and (ii), we get
AC + CB = DC + CE
⇒ AB = DE
APPEARS IN
संबंधित प्रश्न
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
line segment
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
In how many points a line, not in a plane, can intersect the plane?
Boundaries of surfaces are ______.
A pyramid is a solid figure, the base of which is ______.
Euclid belongs to the country ______.
The edges of a surface are curves.
The statements that are proved are called axioms.
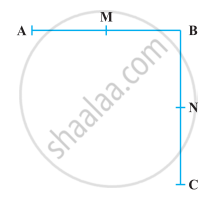
In the following figure AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.
The following statement is true or false? Give reason for your answer.
In the following figure, if AB = PQ and PQ = XY, then AB = XY.

