Advertisements
Advertisements
Question
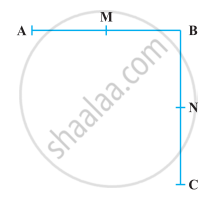
In the following figure BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

Solution
Given, BM = BN ...(i)
M is the mid-point of AB.
∴ AM = BM = `1/2` AB
⇒ 2AM = 2BM = AB ...(ii)
And N is the mid-point of BC.
∴ BN = NC = `1/2` BC
⇒ 2BN = 2NC = BC ...(iii)
According to Euclid’s axiom, things which are double of the same thing are equal to one another.
On multiplying both sides of equation (i) by 2, we get
2BM = 2BN
⇒ AB = BC ...[Using equations (ii) and (iii)]
APPEARS IN
RELATED QUESTIONS
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
line segment
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
square
Given three distinct points in a plane, how many lines can be drawn by joining them?
The three steps from solids to points are ______.
The number of dimensions, a surface has ______.
A pyramid is a solid figure, the base of which is ______.
In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for ______.
In the following figure AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.
Read the following statements which are taken as axioms:
- If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
- If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
The following statement is true or false? Give reason for your answer.
In the following figure, if AB = PQ and PQ = XY, then AB = XY.

