Advertisements
Advertisements
प्रश्न
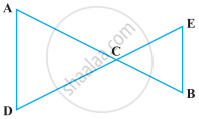
In the following figure BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

उत्तर
Given, BM = BN ...(i)
M is the mid-point of AB.
∴ AM = BM = `1/2` AB
⇒ 2AM = 2BM = AB ...(ii)
And N is the mid-point of BC.
∴ BN = NC = `1/2` BC
⇒ 2BN = 2NC = BC ...(iii)
According to Euclid’s axiom, things which are double of the same thing are equal to one another.
On multiplying both sides of equation (i) by 2, we get
2BM = 2BN
⇒ AB = BC ...[Using equations (ii) and (iii)]
APPEARS IN
संबंधित प्रश्न
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
How many lines can be drawn through both of the given points?
The three steps from solids to points are ______.
A pyramid is a solid figure, the base of which is ______.
The edges of a surface are curves.
The statements that are proved are called axioms.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Solve the following question using appropriate Euclid’s axiom:
Two salesmen make equal sales during the month of August. In September, each salesman doubles his sale of the month of August. Compare their sales in September.
Solve the following question using appropriate Euclid’s axiom:
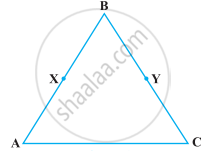
In the following figure, we have BX = `1/2` AB, BY = `1/2` BC and AB = BC. Show that BX = BY.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AC = DC, CB = CE. Show that AB = DE.