Advertisements
Advertisements
प्रश्न
Solve the following question using appropriate Euclid’s axiom:
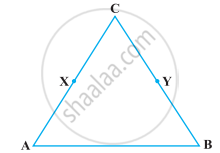
In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
उत्तर
Given, X is the mid-point of AC
AX = CX = `1/2` AC
⇒ 2AX = 2CX = AC ...(i)
And Y is the mid-point of BC.
BY = CY = `1/2` BC
⇒ 2BY = 2CY = BC ...(ii)
Also, given AX = CY ...(iii)
According to Euclid’s axiom, things which are double of the same things are equal to one another.
From equation (iii), 2AX = 2CY
⇒ AC = BC ...[From equation (i) and (ii)]
APPEARS IN
संबंधित प्रश्न
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
parallel lines
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
How many planes can be made to pass through a line and a point not on the line?
Boundaries of solids are ______.
In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio ______.
In ancient India, the shapes of altars used for household rituals were ______.
Greek’s emphasised on ______.
In Ancient India, Altars with combination of shapes like rectangles, triangles and trapeziums were used for ______.
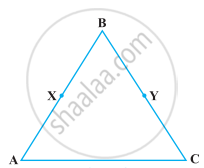
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
Read the following statement :
An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.
