Advertisements
Advertisements
प्रश्न
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
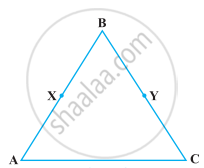
उत्तर
We have, AB = BC ...(i)
And BX = BY ...(ii)
According to Euclid’s axiom, if equals are subtracted from equals, the remainders are equal.
So, on subtracting equation (ii) from equation (i), we get
AB – BX = BC – BY
⇒ AX = CY ...[From figure]
APPEARS IN
संबंधित प्रश्न
If a point C lies between two points A and B such that AC = BC, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
In how many lines two distinct planes can intersect?
How many planes can be made to pass through three distinct points?
The number of dimensions, a solid has ______.
The total number of propositions in the Elements are ______.
Boundaries of solids are ______.
In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio ______.
In ancient India, the shapes of altars used for household rituals were ______.
The things which are double of the same thing are equal to one another.
The following statement is true or false? Give reason for your answer.
There are an infinite number of lines which pass through two distinct points.
