Advertisements
Advertisements
प्रश्न
In how many lines two distinct planes can intersect?
उत्तर
If we look at two intersecting plane, we can see that there is only one unique line at which the two planes intersect.

Therefore, two distinct planes can intersect each other at a single unique line as only a single line is common between two intersecting planes.
APPEARS IN
संबंधित प्रश्न
Consider two ‘postulates’ given below:-
- Given any two distinct points A and B, there exists a third point C which is in between A and B.
- There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
If a point C lies between two points A and B such that AC = BC, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
How many lines can be drawn through both of the given points?
How many lines can be drawn through a given point.
Given three distinct points in a plane, how many lines can be drawn by joining them?
How many planes can be made to pass through two points?
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have AB = BC, BX = BY. Show that AX = CY.
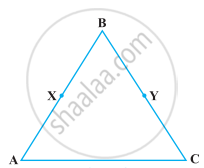
Solve the following question using appropriate Euclid’s axiom:
In the following figure, if OX = `1/2` XY, PX = `1/2` XZ and OX = PX, show that XY = XZ.
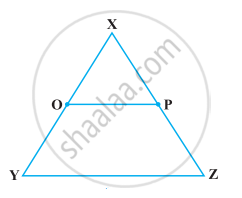
Read the following two statements which are taken as axioms:
- If two lines intersect each other, then the vertically opposite angles are not equal.
- If a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°.
Is this system of axioms consistent? Justify your answer.
The following statement is true or false? Give reason for your answer.
If two circles are equal, then their radii are equal.
