Advertisements
Advertisements
प्रश्न
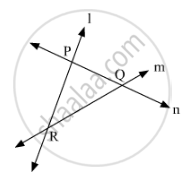
Given three distinct points in a plane, how many lines can be drawn by joining them?
उत्तर
Given three distinct points A, B and C in a plane, they can either be collinear or non collinear.
If they are collinear, then there can be only one line joining them.

If they are non collinear, then there can be three lines joining them.
For example, if we have three distinct non collinear points P, Q and R. Then we can draw three lines l, mand n joining them.
APPEARS IN
संबंधित प्रश्न
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
square
The three steps from solids to points are ______.
The number of dimension, a point has ______.
Greek’s emphasised on ______.
Thales belongs to the country ______.
“For every line l and for every point P not lying on a given line l, there exists a unique line m passing through P and parallel to l ” is known as Playfair’s axiom.
Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.
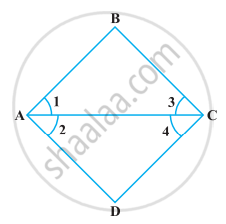
Solve the following question using appropriate Euclid’s axiom:
In the following figure, if OX = `1/2` XY, PX = `1/2` XZ and OX = PX, show that XY = XZ.
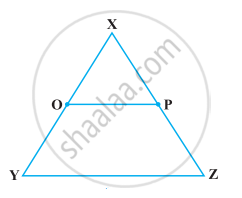
The following statement is true or false? Give reason for your answer.
A terminated line can be produced indefinitely on both the sides.
The following statement is true or false? Give reason for your answer.
If two circles are equal, then their radii are equal.
