Advertisements
Advertisements
प्रश्न
Given three distinct points in a plane, how many lines can be drawn by joining them?
उत्तर
Given three distinct points A, B and C in a plane, they can either be collinear or non collinear.
If they are collinear, then there can be only one line joining them.

If they are non collinear, then there can be three lines joining them.
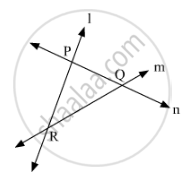
For example, if we have three distinct non collinear points P, Q and R. Then we can draw three lines l, mand n joining them.
APPEARS IN
संबंधित प्रश्न
The following statement is true or false? Give reason for your answer.
Only one line can pass through a single point.
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
parallel lines
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
radius of a circle
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
square
If a point C lies between two points A and B such that AC = BC, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
How many lines can be drawn through a given point.
Euclid divided his famous treatise “The Elements” into ______.
The edges of a surface are curves.
If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.
Read the following axioms:
- Things which are equal to the same thing are equal to one another.
- If equals are added to equals, the wholes are equal.
- Things which are double of the same thing are equal to one another.
Check whether the given system of axioms is consistent or inconsistent.
