Advertisements
Advertisements
प्रश्न
In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio ______.
पर्याय
1 : 3 : 4
4 : 2 : 1
4 : 4 : 1
4 : 3 : 2
उत्तर
In Indus Valley Civilisation (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio 4 : 2 : 1.
Explanation:
In Indus Valley Civilisation, the bricks used for construction work were having dimensions in the ratio length : breadth : thickness = 4 : 2 : 1.
APPEARS IN
संबंधित प्रश्न
Give a definition of the following term. Are there other terms that need to be defined first? What are they, and how might you define them?
radius of a circle
If a point C lies between two points A and B such that AC = BC, then prove that AC = `1/2` AB. Explain by drawing the figure.
If a point C lies between two points A and B such that AC = BC, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Euclid divided his famous treatise “The Elements” into ______.
The side faces of a pyramid are ______.
The statements that are proved are called axioms.
Solve the following question using appropriate Euclid’s axiom:
Look at the figure. Show that length AH > sum of lengths of AB + BC + CD.

Solve the following question using appropriate Euclid’s axiom:
In the following figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.
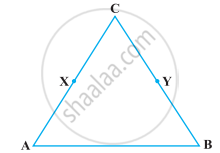
Read the following statement :
An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each.
Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.
Read the following statements which are taken as axioms:
- If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.
- If a transversal intersect two parallel lines, then alternate interior angles are equal.
Is this system of axioms consistent? Justify your answer.
