Advertisements
Advertisements
प्रश्न
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then RP = ______.
उत्तर
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then RP = ZY.
APPEARS IN
संबंधित प्रश्न
Classify the given triangle based on its sides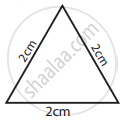
Classify the following triangle based on its sides and angles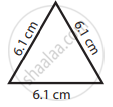
Can a triangle be formed with the following sides? If yes, name the type of triangle.
3.5 cm, 3.5 cm, 3.5 cm
The given triangle is _________
Measures of each of the angles of an equilateral triangle is ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠R = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QR = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠P = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠Q = ______.
If M is the mid-point of a line segment AB, then we can say that AM and MB are congruent.
It is possible to have a triangle in which each angle is equal to 60°.
A one rupee coin is congruent to a five rupee coin.
If three angles of two triangles are equal, triangles are congruent.
If two angles and a side of a triangle are equal to two angles and a side of another triangle, then the triangles are congruent.
