Advertisements
Advertisements
प्रश्न
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠R = ______.
उत्तर
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠R = ∠Z.
APPEARS IN
संबंधित प्रश्न
Classify the given triangle based on its sides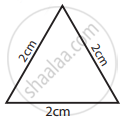
Can a triangle be formed with the following sides? If yes, name the type of triangle.
3.5 cm, 3.5 cm, 3.5 cm
I am a closed figure with each of my three angles is 60°. Who am I?
The given triangle is _________
An equilateral triangle is
If for ∆ABC and ∆DEF, the correspondence CAB `leftrightarrow` EDF gives a congruence, then which of the following is not true?
Measures of each of the angles of an equilateral triangle is ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QR = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠P = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then QP = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then ∠Q = ______.
If ∆PQR and ∆XYZ are congruent under the correspondence QPR `leftrightarrow` XYZ, then RP = ______.
A one rupee coin is congruent to a five rupee coin.
If two sides and one angle of a triangle are equal to the two sides and angle of another triangle, then the two triangles are congruent.
If two angles and a side of a triangle are equal to two angles and a side of another triangle, then the triangles are congruent.
