English Medium
Academic Year: 2024-2025
Date: March 2025
Advertisements
General Instructions:
Read the following instructions carefully and follow them:
- This question paper contains 38 questions.
- This Question Paper is divided into 5 Sections A, B, C, D and E.
- In Section A, Questions no. 1-18 are multiple choice questions (MCQs) and questions no. 19 and 20 are Assertion- Reason based questions of 1 mark each.
- In Section B, Questions no. 21-25 are very short answer (VSA) type questions, carrying 02 marks each.
- In Section C, Questions no. 26-31 are short answer (SA) type questions, carrying 03 marks each.
- In Section D, Questions no. 32-35 are long answer (LA) type questions, carrying 05 marks each.
- In Section E, Questions no. 36-38 are case study based questions carrying 4 marks each with sub parts of the values of 1, 1 and 2 marks each respectively.
- All Questions are compulsory. However, an internal choice in 2 Questions of section B, 2 Questions of section C and 2 Questions of section D has been provided. And internal choice has been provided in all the 2 marks questions of Section E.
- Draw neat and clean figures wherever required.
- Take `pi =22/7` wherever required if not stated.
- Use of calculators is not allowed.
HCF OF (33 × 52 × 2), (32 × 53 × 22) and (34 × 5 × 23) is _________.
450
90
180
630
Chapter:
The system of linear equations represented by lines l and m is _________.

consistent with unique solution
inconsistent
consistent with three solutions
consistent with many solutions
Chapter:
The value of k for which the quadratic equation kx2 − 5x + 1 = 0 does not have a real solution, is __________.
0
`25/4`
`4/25`
7
Chapter:
The distance between the points (a, b) and (−a, −b) is ____________.
`sqrt(a^2 + b^2)`
a2 + b2
`2sqrt(a^2 + b^2)`
`4sqrt(a^2 + b^2)`
Chapter:
In the given figure, PQ and PR are tangents to a circle centred at O. If ∠QPR = 35° then ∠QOR is equal to ________.

70°
90°
135°
145°
Chapter:
If △ABC ∼ △PQR such that 3AB = 2PQ and BC = 10 cm, then length QR is equal to ________.
10 cm
15 cm
`20/3` cm
30 cm
Chapter:
If 3 cot A = 4, where 0° < A < 90°, then sec A is equal to _________.
`5/4`
`4/3`
`5/3`
`3/4`
Chapter:
In the given figure, ΔBAC is similar to ________.
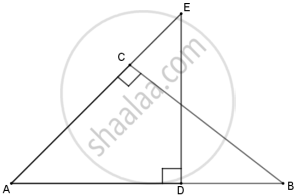
ΔAED
ΔEAD
ΔACB
ΔBCA
Chapter:
If H.C.F (420, 189) = 21 then L.C.M (420, 189) is _________.
420
1890
3780
3680
Chapter:
The 4th term from the end of the A.P. −8, −5, −2, …, 49 is _________.
37
40
1
43
Chapter:
In the given figure, if ΔOCA ∼ ΔOBD, then ∠OAC is equal to ______.
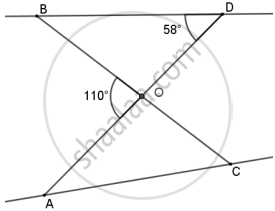
58°
55°
128°
52°
Chapter:
If perimeter of given triangle is 38 cm, then length AP is equal to _________.
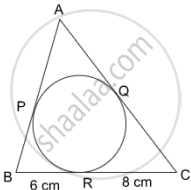
19 cm
5 cm
10 cm
8 cm
Chapter:
`(1 - tan^2 30°)/(1 + tan^2 30°)` is equal to _________.
cos 60°
sin 60°
1
tan260°
Chapter:
The total surface area of a solid hemisphere of radius r is ________.
47πr2
2πr2
`4/3`πr3
3πr2
πr2
4πr2
Chapter: [0.062] Surface Areas and Volumes
Which of the following cannot be the probability of an event?
0.4
4%
0.04%
4
Chapter:
The roots of quadratic equation `3 x^2 − 4sqrt3x + 4` = 0 are ___________.
not real
real and equal
rational and distinct
irrational and distinct
Chapter:
Advertisements
The following distribution shows the marks distribution of 80 students.
| Marks | Below 10 | Below 20 | Below 30 | Below 40 | Below 50 | Below 60 |
| No. of students | 2 | 12 | 28 | 56 | 76 | 80 |
The median class is ________.
20 - 30
40 - 50
30 - 40
10 - 20
Chapter:
A quadratic polynomial whose zeroes are `2/5` and `(-1)/5` is ____________.
25x2 + 5x − 2
5x2 − 2x + 1
5x2 + 2x − 1
25x2 − 5x − 2
Chapter:
Assertion(A): The sequence −1, −1, −1, ......, −1 is an AP.
Reason(R): In an AP, an − an−1 is constant where n ≥ 2 and n ∈ N.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
Chapter:
Assertion(A): `(2 + sqrt3)sqrt3` is an irrational number.
Reason(R): Product of two irrational numbers is always irrational.
Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Assertion (A) is true but reason (R) is false.
Assertion (A) is false but reason (R) is true.
Chapter:
P(x, y) is a point equidistant from the points A(4, 3) and B(3, 4). Prove that x − y = 0.
Chapter:
In the given figure, ΔABC is an equilateral triangle. Coordinates of vertices A and B are (0, 3) and (0, −3), respectively. Find the coordinates of points C.
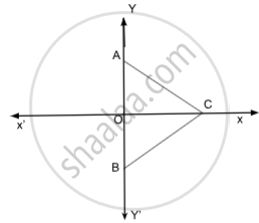
Chapter:
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
Chapter: [0.042] Circles
The sum of the first 12 terms of an A.P. is 900. If its first term is 20, then find the common difference and 12th term.
Chapter:
The sum of the first n terms of an A.P. is represented by Sn = 6n − n2. Find the common difference.
Chapter:
If sin(A − B) = `1/2` and cos(A + B) = `1/2`, 0° < A + B < 90° and A > B, then find the values of A and B.
Chapter:
Calculate mode of the following distribution:
| Class | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 - 30 | 30 - 35 |
| Frequency | 5 | 6 | 15 | 10 | 5 | 4 |
Chapter:
Prove that `sqrt(5)` is an irrational number.
Chapter: [0.011000000000000001] Real Numbers
Find the ratio in which the y-axis divides the line segment joining the points (4, −5) and (−1, 2). Also find the point of intersection.
Chapter:
Advertisements
Line 4x + y = 4 divides the line segment joining the points (−2, −1) and (3, 5) in a certain ratio. Find the ratio.
Chapter:
Prove that (cosec A − sin A) (sec A − cos A) = `1/(tan A + cot A)`.
Chapter:
Find the mean using the step deviation method.
| Class | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 |
| Frequency | 6 | 10 | 15 | 9 | 10 |
Chapter:
In the given figure, PA and PB are tangents to a circle centred at O. Prove that
- OP bisects ∠APB
- OP is the right bisector of AB.
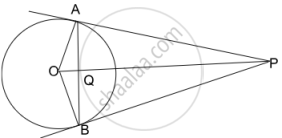
Chapter:
Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Chapter: [0.042] Circles
The sum of a two-digit number and the number obtained by reversing the order of its digits is 99. If ten’s digit is 3 more than the unit’s digit, then find the number.
Chapter:
Amita buys some books for ₹ 1920. If she had bought 4 more books for the same amount each book would cost her ₹ 24 less. How many books did she buy? What was the initial price of one book?
Chapter:
A train travels at a certain average speed for a distance of 132 km and then travels a distance of 140 km at an average speed of 4 km/h more than the initial speed. If it takes 4 hours to complete the whole journey, what was the initial average speed? Determine the time taken by train to cover the distances separately.
Chapter:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.
Chapter:
The perimeter of sector OACB of the circle centred at O and of radius 24, is 73.12 cm.
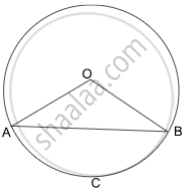
- Find the central angle ∠AOB.
- Find the area of the minor segment ACB. (Use π = 3.14 and `sqrt3` = 1.73)
Chapter:
From the top of a 9 m high building, the angle of elevation of the top of a cable tower is 60° and angle of depression of its foot is 45°. Determine the height of the tower and distance between building and tower. `("Use" sqrt3 = 1.732)`
Chapter:
As observed from the top of a 75 m high lighthouse from the sea level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. `("Use" sqrt3 = 1.732)`
Chapter:
|
A group of students conducted a survey to find out about the preferred mode of transportation to school among their classmates. They surveyed 200 students from their school. The results of the survey are as follows: 120 students preferred to walk to school. 25% of the students preferred to use bicycles. 10% of the students preferred to take the bus. Remaining students preferred to be dropped off by car. |
Based on the above information, answer the following questions:
- What is the probability that a randomly selected student does not prefer to walk to school?
- Find the probability of a randomly selected student who prefers to walk or use a bicycle.
-
- One day 50% of walking students decided to come by bicycle. What is the probability that a randomly selected student comes to school using a bicycle on that day?
OR - What is the probability that a randomly selected student prefers to be dropped off by car?
- One day 50% of walking students decided to come by bicycle. What is the probability that a randomly selected student comes to school using a bicycle on that day?
Chapter:
Radha, an aspiring landscape designer, is tasked with creating a visually captivating pool design that incorporates a unique arrangement of fountains. The challenge entails arranging the fountains in such a way that when water is thrown upwards, it forms the shape of a parabola. The graph of one such parabola is given below.

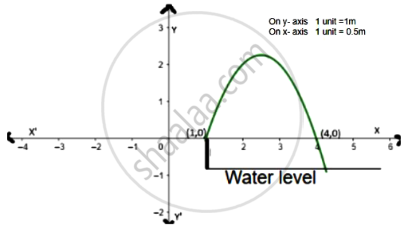
The height of each fountain rod above water level is 10 cm. The equation of the downward-facing parabola representing the water fountain is given by p(x) = −x2 + 5x − 4.
Based on the above information, answer the following questions:
- Find the zeroes of the polynomial p(x) from the graph.
- Find the value of x at which water attains maximum height.
-
- If h is the maximum height attained by the water stream from the water level of the pool, then find the value of h.
OR - At what point(s) on x- axis, the height of water above x- axis is 2 m?
- If h is the maximum height attained by the water stream from the water level of the pool, then find the value of h.
Chapter:
|
Rinku was very happy to receive a fancy jumbo pencil from his best friend Rohan on his birthday. Pencil is a basic writing tool, when sharpened its shape is a combination of cylinder & cone as given in the picture. Cylindrical pencil with conical head is a common shape worldwide since ages. Commonly pencils are made up of wood & plastic but we should promote pencils made up of eco-friendly material (many options available in the market these days) to save environment.
The dimensions of Rinku’s pencil are given as follows: Length of cylindrical portion is 21 cm. Diameter of the base is 1 cm and height of the conical portion is 1.2 cm. |
Based on the above information, answer the following questions:
- Find the slant height of the sharpened part.
- Find curved surface area of sharpened part (in terms of π).
-
- Find the total surface area of the pencil (in terms of π)
OR - The pencil’s total height decreases by 8.2 cm after sharpening it many times, what is the volume of the cylindrical part of the shortened pencil (in terms of π)?
- Find the total surface area of the pencil (in terms of π)
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
CBSE previous year question papers Class 10 Mathematics with solutions 2024 - 2025
Previous year Question paper for CBSE Class 10 Maths-2025 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of CBSE Class 10.
How CBSE Class 10 Question Paper solutions Help Students ?
• Question paper solutions for Mathematics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.

