Advertisements
Advertisements
Question
As observed from the top of a 75 m high lighthouse from the sea level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships. `("Use" sqrt3 = 1.732)`
Sum
Solution
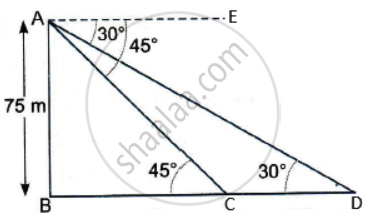
Let AB be the lighthouse and the two ships be at points C and D, respectively.
In ΔABC,
tan 45° = `(AB)/(BC)`
1 = `(75m)/(BC)`
BC = 75 m
In ΔABD,
tan 60° = `(AB)/(BD)`
`1/sqrt3 = 75/(BC + CD)`
`1/sqrt3 = 75/(75 + CD)`
75 + CD = `75sqrt3`
CD = `75 sqrt3 - 75`
CD = `75(sqrt3-1)`
CD = 75(1.732 − 1)
CD = 75 × 0.732
∴ CD = 54.9 m
Hence, the Distance between the two ships is 54.9 m.
shaalaa.com
Is there an error in this question or solution?
