Advertisements
Advertisements
Question
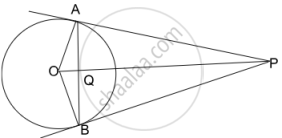
In the given figure, PA and PB are tangents to a circle centred at O. Prove that
- OP bisects ∠APB
- OP is the right bisector of AB.
Sum
Solution
i. ΔOAP ≅ ΔOBP
∠APO = ∠BPO
Or OP bisects ∠P
ii. ΔAQP ≅ ΔBQP
⇒ AQ = QB and ∠AQP = ∠BQP
AB is a straight line.
Therefore, ∠AQP = ∠BQP = 90°
Hence, OP is the right bisector of AB.
shaalaa.com
Is there an error in this question or solution?
