Advertisements
Advertisements
प्रश्न
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
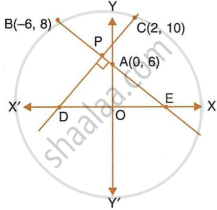
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
उत्तर
In the given figure, AB meets y-axis at point A.
Line through C(2, 10) and D intersects line AB at P at right angle.
i. Slope of AB (m) = `(y_2 - y_1)/(x_2 - x_1)`
= `(8 - 6)/(-6 - 0)`
= `2/(-6)`
= `(-1)/3`
∴ Equation of line AB is given by
y – y1 = m(x – x1)
`\implies y - 6 = (-1)/3(x - 0)`
`\implies` 3y – 18 = –x
`\implies` x + 3y – 18 = 0
`\implies` x + 3y = 18 ...(1)
ii. ∵ CD ⊥ AB
∴ Slope of line CD = `-(3/(-1))` = 3 ...[∵ m1m2 = –1]
∴ Equation of CD is given by
y – 10 = 3(x – 2)
`\implies` y – 10 = 3x – 6
`\implies` 3x – y + 10 – 6 = 0
`\implies` 3x – y + 4 = 0 ...(2)
iii. Since equation (2) meets x-axis at D
∴ Putting y = 0 in 3x – y + 4 = 0
`\implies` 3x – 0 + 4 = 0
`\implies` 3x + 4 = 0
`\implies` 3x = −4
`\implies x = (-4)/3`
∴ Co-ordinates of D are `((-4)/3, 0)`
∵ Since equation (1) meets x-axis at E, so putting
y = 0 in x + 3y = 18
∴ x + 0 = 18 `\implies` x = 18
∴ Co-ordinates of E are (18, 0).
APPEARS IN
संबंधित प्रश्न
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Given 3x + 2y + 4 = 0
(i) express the equation in the form y = mx + c
(ii) Find the slope and y-intercept of the line 3x + 2y + 4 = 0
Find the slope and y-intercept of the line:
ax – by = 0
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find:
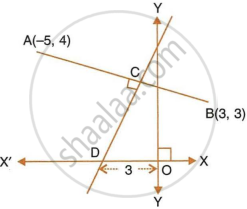
- equation of AB
- equation of CD
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
