Advertisements
Advertisements
प्रश्न
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
उत्तर
For the line AB:
Slope of AB = m = `(2 - 0) /(2 - 4) = 2/(-2)= -1 `
(x1, y1) = (4, 0)
Equation of the line AB is
y − y1 = m(x − x1)
y − 0 = −1(x − 4)
y = −x + 4
x + y = 4 ...(1)
For the line BC:
Slope of BC = m = `(6 - 2)/(0 - 2) = 4/(-2) = -2`
(x1, y1) = (2, 2)
Equation of the line BC is
y − y1 = m(x − x1)
y − 2 = −2(x − 2)
y − 2 = −2x + 4
2x + y = 6 ...(2)
Given that AB cuts the y-axis at P.
So, the abscissa of point P is 0.
Putting x = 0 in (1), we get,
y = 4
Thus, the co-ordinates of point P are (0, 4).
Given that BC cuts the x-axis at Q.
So, the ordinate of point Q is 0.
Putting y = 0 in (2), we get,
2x = 6
`=>` x = 3
Thus, the co-ordinates of point Q are (3, 0).
APPEARS IN
संबंधित प्रश्न
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
3x – 4y = 5
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
Find the equation of the line which is perpendicular to the line `x/a - y/b = 1` at the point where this line meets y-axis.
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
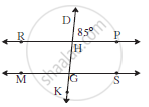
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
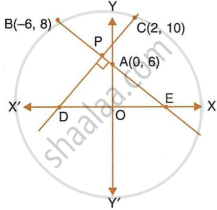
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
