Advertisements
Advertisements
प्रश्न
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
उत्तर
We know that in a rhombus, diagonals bisect each other at right angle.
Let O be the point of intersection of the diagonals AC and BD.
Co-ordinates of O are
`((-5 + 1)/2, (6 + 4)/2) = (-2, 5)`
Slope of BD = `(4 - 6)/(1 + 5) = (-2)/6 = (-1)/3`
For line BD:
Slope = m = `(-1)/3`, (x1, y1) = (–5, 6)
Equation of the line BD is
y – y1 = m(x – x1)
`y - 6 =(-1)/3 (x + 5)`
3y – 18 = –x – 5
x + 3y = 13
For line AC:
Slope = m `(-1)/"slope of BD"` = 3, (x1, y1) = (–2, 5)
Equation of the line AC is
y − y1 = m(x − x1)
y − 5 = 3(x + 2)
y − 5 = 3x + 6
y = 3x + 11
APPEARS IN
संबंधित प्रश्न
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
Find the slope and y-intercept of the line:
y = 4
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
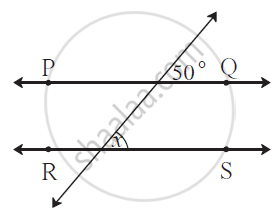
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
