Advertisements
Advertisements
प्रश्न
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
उत्तर
4x + 5y = 6
5y = −4x + 6
`y = (-4x)/5 + 6/5`
Slope of this line = `(-4)/5`
The required line is perpendicular to the line 4x + 5y = 6.
∴ Slope of the required line = `(-1 )/"slope of the given line"`
= `(-1)/((-4)/5)`
= `5/4`
The required equation of the line is given by
y − y1 = m(x − x1)
`y − 1 = 5/4 (x + 2)`
4y − 4 = 5x + 10
5x − 4y + 10 + 4 = 0
5x − 4y + 14 = 0
APPEARS IN
संबंधित प्रश्न
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Find the slope and y-intercept of the line:
y = 4
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
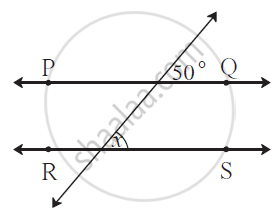
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
Find Equation of CD
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
