Question

Prove that: If the angles of a triangle are 45° – 45° – 90°^, then each of the perpendicular sides is \[\frac{1}{\sqrt{2}}\]times the hypotenuse.”

 

Answer 1

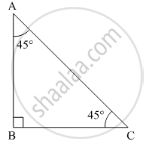
Let ABC be the required triangle with 

\[\angle\]B = 90º and

\[\angle\]A = 

\[\angle\]C = 45º.

To prove: 

\[AB = BC = \frac{1}{\sqrt{2}}AC\]

Proof: 

\[\angle\]A = 

\[\angle\]C = 45º

So, AB = BC              (Sides opposite to equal angles are equal)

\[{AB}^2 + {BC}^2 = {AC}^2 \]
\[ \Rightarrow {AB}^2 + {AB}^2 = {AC}^2 \]
\[ \Rightarrow 2 {AB}^2 = {AC}^2 \]
\[ \Rightarrow AB = \frac{1}{\sqrt{2}}AC\]
\[ \Rightarrow AB = BC = \frac{1}{\sqrt{2}}AC\]