Advertisements
Advertisements
Question
Construct a triangle similar to a given triangle ABC with its sides equal to `6/5` of the corresponding sides of the triangle ABC (scale factor `6/5 > 1`)
Solution
Given triangle ∆ABC, we are required to construct another triangle whose sides are `6/5` of the corresponding sides of the ∆ABC.
Steps of construction:
(i) Construct an ∆ABC with any measurement.
(ii) Draw a ray BX making an acute angle with BC.
(iii) Locate 6 points Q1, Q2, Q3, Q4, Q5, Q6 on BX such that
BQ1 = Q1Q2 = Q2Q3 = Q3Q4 = Q5Q6 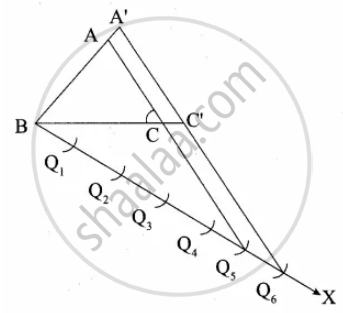
(iv) Join Q5 to C and draw a line through Q6 parallel to Q5 C intersecting the extended line BC at C’.
(v) Draw a line through C’ parallel to AC intersecting the extended line segment AB at A’.
∴ ∆A’BC’ is the required triangle.
APPEARS IN
RELATED QUESTIONS
In ∆ABC, DE is parallel to base BC, with D on AB and E on AC. If `\frac{AD}{DB}=\frac{2}{3}` , find `\frac{BC}{DE}.`
Using Basic proportionality theorem, prove that a line drawn through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

In the given figure, ∠PQR = ∠PST = 90° ,PQ = 5cm and PS = 2cm.
(i) Prove that ΔPQR ~ ΔPST.
(ii) Find Area of ΔPQR : Area of quadrilateral SRQT.

ΔABC is enlarged, with a scale factor 5. Find: BC, f B'C' = 16cm
If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
D is the mid point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that b2 = `"p"^2 + "a"x + "a"^2/4`
From the given figure, prove that ΔABC ~ ΔEDF
ΔABC and ΔBDE are two equilateral triangles such that D is the mid point of BC. Ratio of the areas of triangle ΔABC and ΔBDE is ______.
