Advertisements
Advertisements
Question
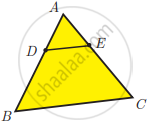
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x – 7, DB = 5x – 3, AE = 4x – 3 and EC = 3x – 1, find the value of x
Solution
Given AD = 8x – 7; BD = 5x – 3; AE = 4x – 3; EC = 3x – 1
In ∆ABC we have DE || BC
By Basic proportionality theorem
`"AD"/"DB" = "AE"/"EC"`
`(8x - 7)/(5x - 3) = (4x - 3)/(3x - 1)`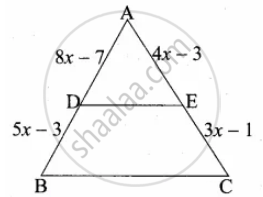
(8x – 7) (3x – 1) = (4x – 3) (5x – 3)
24x2 – 8x – 21x + 7 = 20x2 – 12x – 15x + 9
24x2 – 20x2 – 29x + 27x + 7 – 9 = 0
4x2 – 2x – 2 = 0
2x2 – x – 1 = 0 ...(Divided by 2)
2x2 – 2x + x – 1 = 0
2x(x – 1) + 1 (x – 1) = 0
(x – 1) (2x + 1) = 0
x – 1 = 0 or 2x + 1 = 0
x = 1 or 2x = – 1 ⇒ x = `– 1/2` ...(Negative value will be omitted)
The value of x = 1
APPEARS IN
RELATED QUESTIONS
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.
If PQ || BC and PR || CD prove that `"AR"/"AD" = "AQ"/"AB"`
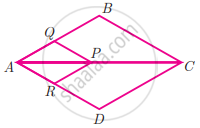
If PQ || BC and PR || CD prove that `"QB"/"AQ" = "DR"/"AR"`
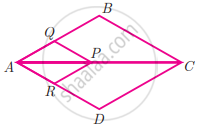
In trapezium ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that = `"AE"/"ED" = "BF"/"FC"`
∠QPR = 90°, PS is its bisector. If ST ⊥ PR, prove that ST × (PQ + PR) = PQ × PR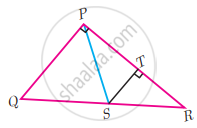
Construct a ∆PQR in which the base PQ = 4.5 cm, ∠R = 35° and the median from R to RG is 6 cm.
Construct a ∆PQR such that QR = 6.5 cm, ∠P = 60° and the altitude from P to QR is of length 4.5 cm
Draw a triangle ABC of base BC = 5.6 cm, ∠A = 40° and the bisector of ∠A meets BC at D such that CD = 4 cm
ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is
ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE. Show that the points B, C, E and D lie on a same circle