Advertisements
Advertisements
Question
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB" = 3/4` and AC = 15 cm find AE
Solution
Let AE be x
∴ EC = 15 – x
In ∆ABC we have DE || BC
By Basic proportionality theorem, we have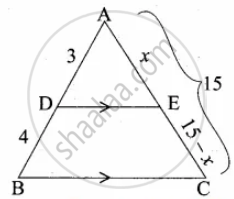
`"AD"/"DB" = "AE"/"EC"`
`3/4 = x/(15 - x)`
4x = 3(15 – x)
4x = 45 – 3x
7x = 45
⇒ x = `45/7`
= 6.43
The value of x = 6.43
APPEARS IN
RELATED QUESTIONS
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If AD = 8x – 7, DB = 5x – 3, AE = 4x – 3 and EC = 3x – 1, find the value of x
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.
Rhombus PQRB is inscribed in ΔABC such that ∠B is one of its angle. P, Q and R lie on AB, AC and BC respectively. If AB = 12 cm and BC = 6 cm, find the sides PQ, RB of the rhombus.
In trapezium ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that = `"AE"/"ED" = "BF"/"FC"`
∠QPR = 90°, PS is its bisector. If ST ⊥ PR, prove that ST × (PQ + PR) = PQ × PR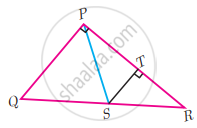
ABCD is a quadrilateral in which AB = AD, the bisector of ∠BAC and ∠CAD intersect the sides BC and CD at the points E and F respectively. Prove that EF || BD.
Construct a ∆PQR in which QR = 5 cm, ∠P = 40° and the median PG from P to QR is 4.4 cm. Find the length of the altitude from P to QR.
Draw ∆PQR such that PQ = 6.8 cm, vertical angle is 50° and the bisector of the vertical angle meets the base at D where PD = 5.2 cm
An Emu which is 8 feet tall is standing at the foot of a pillar which is 30 feet high. It walks away from the pillar. The shadow of the Emu falls beyond Emu. What is the relation between the length of the shadow and the distance from the Emu to the pillar?
Two circles intersect at A and B. From a point, P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
